

![]()

在前面兩單元, 我們介紹了直線排列, 若將直線的首尾相接,變成一個園, 稱之為"環狀", 如下圖:
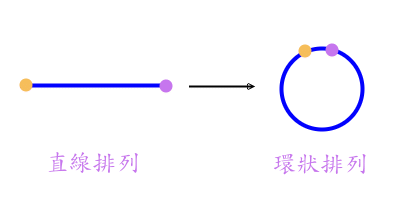
環狀排列: 又稱圓排列, 是將事物沿著一圓周來作排列, 只考慮事物的相對位置, 而不計較
各物件所在的實際位置。 此排列可旋轉, 但不可翻轉。底下先看一個問題:
甲乙丙三人圍一圓桌而坐, 共有幾種坐法?
解這個問題, 我們先考慮甲乙丙三人做直線排列的狀況:
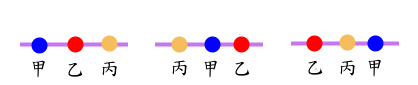
(圖1)

(圖2)
共計6種情形。若將(圖1)的直線排列首尾相接, 成為一圈, 如(圖3)
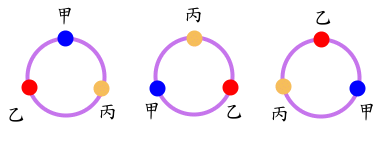
(圖3)
我們可以發現(圖3)的中間與右邊兩圓, 都是左邊的圓逆時針旋轉的結果, 所以應屬於同一類。
同理, 若將(圖2)的直線排列首尾相接, 成為一圓, 如(圖4), 也可發現此三個也屬於同一類。

故共有
所以若 一種。故環狀排列數為 直線排列數/排列之個數。底下我們給出『環狀排列』的公式: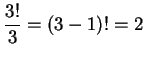 種排列方式。
種排列方式。
![]() 個不同事物在做環狀排列時,
先求其直線排列, 因每
個不同事物在做環狀排列時,
先求其直線排列, 因每![]() 個排列方式中,
在環狀排列均視為同
個排列方式中,
在環狀排列均視為同
接下來我們介紹『項鍊排列』, 因項鍊沒有正反面之分, 所以項鍊排列數就是環狀排列數除以2。
![]()
生活中的實例1
五對夫婦圍圓桌而坐, 試問男女相間坐的方法數為何?
[解]:
先直線排列:
![]()
故環狀排列數為
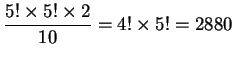 。
。
生活中的實例2
五對夫婦圍圓桌而坐, 試問每對夫妻相鄰而坐的方法數為何?
[解]:
先直線排列: ![]()
故環狀排列數為
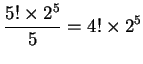 。
。
隨堂練習1
有三男三女圍一圓桌相隔而坐,試問共有幾種不同的坐法。
[解]: 12種。
隨堂練習2
甲、乙、丙、丁、戊、己六人圍一圓桌而坐,若甲、乙、丙三人相鄰而坐, 試問共有幾種不
同的坐法。
[解]: 36種。
生活中的實例3
有8個不同顏色的珠子, 全部串成一項圈, 試問其方法數有多少種?
[解]:
先將其想像成8個不同的物品做環狀排列, 故其方法數有![]() ,
,
其次因項鍊沒有正反面之分, 故須除以2, 所以共有![]() 種。
種。
隨堂練習3
有8個不同顏色的珠子, 取6個串成一項鍊,
試問其方法數有多少種?
[解]:1680種。

1. 四對夫妻圍圓桌而坐, 下列各情況, 各有幾種坐法?
(1) 男女相隔且夫妻相鄰,
(2) 每對夫妻相對,
(3) 恰有三對夫妻相鄰,
(4) 夫妻不相鄰且男女相間隔。
1. (1) 12, (2) 48, (3) 384, (4) 12。