

![]()

在日常生活中, 常會遇到『從一些事物中選出幾個出來, 到底有多少種選法?』的問題。
我們先看下面一個簡單的問題:
在書店賣有4種不同的筆記本, 某人欲從中任選3本, 試問共有幾種選法?
解這個問題時, 我們先將4本筆記本依序編號為A, B, C, D, 如下步驟解之:
第一步: 任取3本做直線排列, 共有![]() 種:
種:
| ABC | ACB | BAC | BCA | CAB | CBA |
| ABD | ADB | BAD | BDA | DAB | DBA |
| ACD | ADC | CAD | CDA | DAC | DCA |
| BCA | BDC | CBD | CDB | DBC | DCB |
第二步: 因筆記本的選取並無先後之考量, 故可將下述視為同一種:
如第一列都是A, B, C三本筆記本在排列, 若選取, 應屬於同一類(A,B,C), 餘類推。
| ABC | ACB | BAC | BCA | CAB | CBA | 屬於(A,B,C) |
| ABD | ADB | BAD | BDA | DAB | DBA | 屬於(A,B,D) |
| ACD | ADC | CAD | CDA | DAC | DCA | 屬於(A,C,D) |
| BCD | BDC | CBD | CDB | DBC | DCB | 屬於(B,C,D) |
所以共有4種選法, 即(A,B,C), (A,B,D), (A,C,D), (B,C,D)。
若以文字來說明, 步驟如下:
(1) 先將這4本筆記本任選3本作直線排列,
其排列數為![]() 。
。
(2) 由於對固定的3本筆記本, 作完全相異物直線排列時, 其排列數為3!, 且皆屬於同一種組合,
因此組合數為
事實上我們可以『相異物組合』的一般形式:
組合![]() 有一些性質, 我們列於下:
有一些性質, 我們列於下:
(1)
![]() 。
。
(2)
![]() 。
。
(3)
![]() 。
。
在組合中, 有一重要的式子, 稱之為『巴斯卡原理』, 其形式與推導如下:
其推導並不難, 只要利用組合的概念, 就可以得到, 推導如下:
![\begin{eqnarray*}
&& C^{n-1}_{m-1}+C^{n-1}_m \\
&& =\frac {(n-1)!}{(m-1)!(n-m)!...
...1)!}{m!(n-m)!}\times [m+(n-m)]\\
&& =\frac {n!}{m!(n-m)!}=C^n_m
\end{eqnarray*}](c2-5/con1-4a/img31.gif)
![]()
生活中的實例1
從六男五女中選出8人組成一訪問團, 試問共有多少種選法。
[解]: 此即組合的一般題型, 故共有
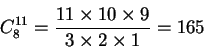 種。
種。
隨堂練習1
某一組織有12人, 從中推舉出5人參加座談會, 試問共有幾種選法?
[解]: 792種。
生活中的實例2
若![]() , 試求
, 試求![]() 之值。
之值。
[解]:
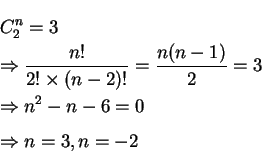
隨堂練習2
設
![]() 。試求
。試求![]() 之值。
之值。
[解]: ![]() ,
, ![]() 。
。
生活中的實例3
從6男5女中, 任選4人組一委員會, 其中至少包含2男1女, 試問共有幾種選法?
[解]: 可能情形: 2男2女, 3男1女, 故共有
隨堂練習3
兄第二人在排成一列的20個空位中, 選坐不相鄰的兩個座位, 試問有多少種坐法。
[解]: 342種。
生活中的實例4
一副撲克牌共有52張, 自中任取5張, 5張為full house (如aaabb)共有多少種?
[解]:
先從13個號碼中選1個: ![]() ,
,
再從選出的號碼中選3種花色: ![]() ,
,
其次從剩下的12個號碼中選一個: ![]() ,
,
從選出的第二個號碼中選2種花色: ![]() ,
,
故共有
![]() 種。
種。
隨堂練習4
一副撲克牌共有52張, 自中任取5張, 5張為三條(如aaabc, 三同二異) 共有多少種?
[解]: ![]() 種。
種。
生活中的實例5
6本不同的書, 按1,2,3分成3堆, 共有幾種方法?
[解]:
先取1本: ![]() ,
,
其次從所剩的5本中任取2本: ![]() ,
,
最後將所剩的3本全取: ![]() ,
,
共總共有
![]() 種。
種。
隨堂練習5
6本不同的書, 按1,2,3隨意分配給甲、乙、丙三人共有多少種方法?
[解]: ![]() 種
種
生活中的實例6
試求
![]() 之值。
之值。
[解]:
因![]() , 故
, 故
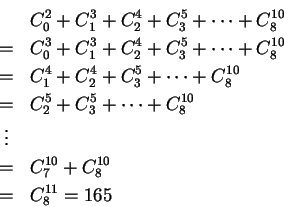
隨堂練習6
試求
![]() 之值。
之值。
[解]: 1140。

某職業籃球隊有球員15人, 每個人有固定打球的位置, 其中中鋒有4人, 後衛有5人, 前鋒有
6人。若一場比賽需上場五名球員, 其中中鋒一名, 後衛二名,前鋒二名, 試問共有幾種不同
的選擇球員的方法?
要在一有十節車廂的火車上, 指定其中三節車廂准許吸煙,兩節車廂放置公共電話。試問
(1) 共有幾種不同方式來放置吸煙區與公共電話區?
(2) 若三節准許吸煙的車廂須兩兩不相接, 則放置准許吸煙的車廂有多少種?
(3) 若吸煙區與公共電話不能在同一車廂, 則有幾種方式?
[解答部分]:
1. 600種。
2. (1) 5400種, (2) 64種, (3) 2520種。

試求
![]() 之值。
之值。
二次方程式
![]() 的兩根為
的兩根為![]() 。試求
。試求![]() 之值。
之值。
投擲一公正骰子三次, 第![]() 次的結果以
次的結果以![]() 表之,
其中
表之,
其中![]() 。試求
。試求![]()
之情形共有多少種?
某次拳擊比賽,規定每位選手必須和所有選手各比賽一場,賽程總計78場,試求選手之人數。
平面上共有14條直線,其中4條共點,而另3條平行。這些直線共可構成多少個三角形。
有兩個凸多邊形,共有16個邊、41條對角線,則此二多邊形的邊數分別為何。
如下圖的14個點,可決定多少個三角形。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[解答部分]
1. 435。
2. ![]() ,
, ![]() 。
。
3. 20。
4. 13人。
5. 326。
6. 7與9。
7. 334。